Fancy CRCing You Here
(Spoiler: short attention havers can follow direct link to results.)
2024 update: somebody reached out to mention they use crcspeed for a tool that runs in control rooms and performs ‘high-rate’ data processing from experiments on the international space station for the European Space Agency. For the ISS project, the CRC is part of our (NASA) interface control documentation.
2021 update: somebody apparently reviewed this article and the redis-related PR results seven years after this page was originally posted 🤷♂️
2018 update: Robert Kausch used the results here to upstream fast crc calculations into the primary ogg and flac libraries. 💪
Redis has a CRC-64 implementation and a lot of people have copied it into other projects.
Redis also has a CRC-16 implementation but fewer people have copied that one.
They work, but they could be better.
after action report: redis decided to ignore these advancements in throughput and reductions in latency because they prefer to code like it’s 1999.
the tradeoff is their outdated legacy design is now 40x slower than it could be otherwise. good job everyone.
if only someone had written a replacement for legacy redis and memcached by now
What’s Wrong
CRCs are inherently non-parallelizable because the C in CRC stands for Cyclical, meaning the value of the next iteration depends depends on the previous iteration. There’s no simple unrolling of loops to process multiple bytes per iteration.
Redis uses CRC-64 in three places:
- adding a checksum when migrating keys across instances
- (and verifying said checksum)
- adding a checksum to RDB output, both for replication and persistence
- (optional, can be disabled by config option because of slow performance)
- user-initiated memory testing
Redis uses CRC-16 in one place:
- hash function for key to cluster slot assignment in Redis Cluster
The Redis implementations are extremely simple. The Redis CRC-64 and CRC-16 functions use the Sarwate method of CRC calculation, which is just a lookup table with the CRC value of every possible byte value1. The lookup table uses a for loop to iterate over input bytes, look up each byte in the table, then generate a final result with O(N) trips through the loop where N is the size of the input in bytes.
What’s Better
I went squiggling around the Internet to see how other people implement CRC-64. It was mostly copies of the Redis source.
One version not from the Redis source appeared hiding inside a stackoverflow comment written by some guy from a few months earlier: an entire custom high-speed CRC-64 implementation. As of this writing, it has 5 upvotes.
I took Mark’s crc64 and compared it with the Redis crc64.
Mark’s version was 400% faster than the Redis version. 1.6 GB/s versus 400 MB/s.
But, the new version didn’t generate the same CRC-64 as CRC Redis uses because there are a dozen different CRC-64 variants and these two aren’t the same.
The CRC results are different because the history of CRC engineering is pretty awful.
From A PAINLESS GUIDE TO CRC ERROR DETECTION ALGORITHMS (1993):
We will call this the REFLECTED algorithm.
Whether or not it made sense at the time, the effect of having reflected algorithms kicking around the world’s FTP sites is that about half the CRC implementations one runs into are reflected and the other half not. It’s really terribly confusing. In particular, it would seem to me that the casual reader who runs into a reflected, table-driven implementation with the bytes “fed in the wrong end” would have Buckley’s chance of ever connecting the code to the concept of binary mod 2 division.
It couldn’t get any more confusing could it? Yes it could.
So, we couldn’t use Mark’s fast version verbatim, but we could see how it works.
What’s Improved
The original Redis CRC-64 slow version using the Sarwate method:
The slow version loops over every byte of input, sequentially.
The new fast version:
while (len >= 8) {
crc ^= *(uint64_t *)byte;
crc = lookup_table[7][crc & 0xff] ^
lookup_table[6][(crc >> 8) & 0xff] ^
lookup_table[5][(crc >> 16) & 0xff] ^
lookup_table[4][(crc >> 24) & 0xff] ^
lookup_table[3][(crc >> 32) & 0xff] ^
lookup_table[2][(crc >> 40) & 0xff] ^
lookup_table[1][(crc >> 48) & 0xff] ^
lookup_table[0][crc >> 56];
byte += 8;
len -= 8;
}
while (len) {
crc = lookup_table[0][(crc ^ *byte++) & 0xff] ^ (crc >> 8);
len--;
}Yes, the fast version looks like a tiger prepping to devour your entrails, but stick with it for a little while.
The fast version loops over the input in 8 byte steps. Any remainder bytes get processed individually at the end (notice how the final cleanup while loop is exactly the same as the original table lookup version, but with the lookup table now part of a multidimensional array).
For a 500 MB input:
- slow version requires 500 million iterations (one for each byte)2.
- fast version runs ~
500 MB/8 B= 62.5 million iterations.
How can the fast version process 8 bytes at once if the current result depends on the value of the previous result?
Notice how the slow version uses a one dimensional uint64_t lookup_table[256], but the fast version uses a two dimensional uint64_t lookup_table[8][256].
The fast version generates a special lookup table containing each possible combined CRC-64 value for each possible byte input. So, instead of one 256 byte lookup table, we have 8 lookup tables each holding another 256 byte lookup table.
The fast version generates the 8x256 lookup table using:
/* FOR LOOP A */
for (n = 0; n < 256; n++) {
crc = n;
/* FOR LOOP B */
for (k = 0; k < 8; k++)
crc = crc & 1 ? POLY ^ (crc >> 1) : crc >> 1;
table[0][n] = crc;
}
/* FOR LOOP C */
for (n = 0; n < 256; n++) {
crc = table[0][n];
/* FOR LOOP D */
for (k = 1; k < 8; k++) {
crc = table[0][crc & 0xff] ^ (crc >> 8);
table[k][n] = crc;
}
}Loop A uses Loop B to generate the CRC-64 for byte n, creating exactly the same contents as the slow lookup table of 256 entries. Notice how Loop A assigns from [0][0] to [0][255]. The original slow lookup table’s values sit in the zero array.
Instead of calculating the initial CRC-64 lookup table ourselves (as Loop B above does), we can use an existing CRC-64 implementation to bootstrap our zero table. This is also the secret of adapting this fast CRC-64 calculation approach to other CRC-64 variants, since the original parameters didn’t match our existing implementation’s output. All we had to use in the beginning was the lookup table from the CRC-64 for Redis—we didn’t have any code to generate the lookup table itself!
Using the “bring your own CRC-64 function” approach, we can change Loop A to:
Now we have a generic CRC-64 acceleration method capable of being adapted to different CRC-64 parameters without changing the underlying implementation— all you need to do is pass in a bootstrap function to provide the initial CRC-64 lookup table of 256 values using your chosen parameters.
Loop C is the secret to speeding up the CRC-64 calculation. Instead of using just one lookup table with 256 entries, we generate seven additional lookup tables, each with 256 entries.
The additional lookup tables hold every combination of CRC values getting applied in the middle of a CRC calculation so we can use “partial CRCs” instead of requiring each future CRC value to fully depend on the previous CRC value.
The “use 8x256 lookup tables” method is called slicing-by-8 and was released in 2006 by researchers at Intel. For a good walkthrough of how and why it works, check out a comparison of fast CRC methods.
We can use slicing-by-8 to calculate our CRC 64 very quickly. Plus, processing 8 bytes at once is a property of the input, not of the CRC width itself (which, with a CRC-64 is also 8 bytes).
Meaning: we can use the same slicing-by-8 trick to speed up CRC-16 calculations too.
Result
crcspeed
The result of all this blathering is, after working at this on and off all year, I finally made a fast CRC-64 implementation matching the CRC-64 variant Redis uses — and — as a bonus, I was also able to add fast CRC-16 calculation.
Moreover, I was able to create or track down implementations of the CRC variants Redis uses instead of only having opaque lookup tables as references.
Now instead of including static lookup tables in the source, we can generate them on startup (much cleaner than leaving dozens or hundreds of static hex constants in headers; plus if we don’t even need the CRC feature but have the CRC library loaded, our process doesn’t need to hold the excess constants—we can generate them as needed instead of always dragging them along as code bloat).
The final result is crcspeed.
Don’t take my word for it; let the numbers speak for themselves.
Benchmark Comparison of crcspeed
% ./crcspeed-test ~/Downloads/John\ Mayer\ -\ Live\ At\ Austin\ City\ Limits\ PBS\ -\ Full\ Concert-gcdUz12FkdQ.mp4
Comparing CRCs against 730.72 MB file...
crc64 (no table)
CRC = ee43263b0a2b6c60
7.142642 seconds at 102.30 MB/s (24.18 CPU cycles per byte)
crc64 (lookup table)
CRC = ee43263b0a2b6c60
1.777920 seconds at 411.00 MB/s (6.02 CPU cycles per byte)
crc64speed
CRC = ee43263b0a2b6c60
0.448819 seconds at 1628.09 MB/s (1.52 CPU cycles per byte)
crc16 (no table)
CRC = 000000000000490f
7.413062 seconds at 98.57 MB/s (25.10 CPU cycles per byte)
crc16 (lookup table)
CRC = 000000000000490f
1.951917 seconds at 374.36 MB/s (6.61 CPU cycles per byte)
crc16speed
CRC = 000000000000490f
0.441418 seconds at 1655.38 MB/s (1.49 CPU cycles per byte)Same Results, But Tabular
| CRC | Method | Time | Throughput | CPU cycles/byte |
|---|---|---|---|---|
| CRC-64-Jones | bit-by-bit | 7.14 seconds | 102 MB/s | 24.18 |
| CRC-64-Jones | lookup table | 1.78 seconds | 411 MB/s | 6.02 |
| CRC-64-Jones | slicing-by-8 | 0.45 seconds | 1,628 MB/s | 1.52 |
| CRC-16-CCITT | bit-by-bit | 7.41 seconds | 98 MB/s | 25.10 |
| CRC-16-CCITT | lookup table | 1.95 seconds | 374 MB/s | 6.61 |
| CRC-16-CCITT | slicing-by-8 | 0.44 seconds | 1,655 MB/s | 1.49 |
…and those results are from my laptop.
Real-World Impact
Why does any of this matter?
When Redis fork()s for RDB creation, COW memory starts to grow at a rate depending on your incoming write load. The sooner Redis finishes writing the RDB, exits the fork()’d child, and returns to normal processing, the less memory you will use due to COW issues.
Redis calculates the CRC for the RDB in the RDB child, so the quicker CRC-64 completes, the less time your RDB child will remain active. The less time your RDB child remains active, the less memory you will use due to COW duplication (applies to replication and on-disk persistence and key migration during Cluster operations since all migrations are checksum’d by CRC-64).
When running a memory test, Redis uses CRC-64 to verify written contents can be read back successfully. Running memory tests 400% faster can make people more inclined to actually test things.
Redis Cluster uses CRC-16 for key-to-cluster-slot mapping. If users are doing wacky things like using 300 MB keys, fast CRC-16 reduces any cluster-slot-assignment overhead by 400%.
It’s an effective and efficient multidimensional win win.
Minor Notes
During my research, I didn’t find any generally available CRC-64 or CRC-16 slicing-by-8 implementation ready to include in other projects or products.
So, I had to create one.
Now we have crcspeed.
crcspeed provides both a framework for enabling any CRC-64 model to use slicing-by-8 as well as allowing any CRC-16 model to use slicing-by-8. All you need is to provide a bootstrap CRC function to generate the initial 256-entry lookup table, then the framework takes care of populating the 8x256 lookup table for you as well doing the slicing-by-8 lookups from the populated table.
crcspeed includes a fast CRC-64-Jones implementation (crc64speed) as well as a fast CRC-16-CCITT implementation (crc16speed).
It’s a new thing. Use it everywhere.
Resources Consulted
CRC theory and implementation are very deep areas. Along the way to getting crcspeed working, I consulted these major resources:
First, a special thanks to the amazing A PAINLESS GUIDE TO CRC ERROR DETECTION ALGORITHMS - it’s what would be now considered “old school” technical writing: text file, well written, well formatted, entertaining, thought out in all dimensions of style, layout, and tone, by experts, for the understanding of others (and themselves).
Another excerpt:
Despite the fact that the above code is probably optimized about as much as it could be, this did not stop some enterprising individuals from making things even more complicated. To understand how this happened, we have to enter the world of hardware.
Somewhere along the way, the Internet lost the ability to hold well written, well formatted, information packed guides, FAQs, and approachable research papers. We should try to get that part of the world back. What’s to blame for that loss? Over reliance on style? CSS? JavaScript? PHP?
Anyway, A PAINLESS GUIDE TO CRC ERROR DETECTION ALGORITHMS convinced me it was hopeless to try and implement CRC-64-Jones myself and I should just find an existing, properly licensed, implementation to use which I found in the excellent pycrc [homepage] utility (also at pycrc [github]).
https://www.kernel.org/doc/Documentation/crc32.txt — yah yah yah the linux kernel uses it to yah yah yah
Special note: The research paper introducing “slicing by 8” was hosted on Intel’s site. The reference is just a URL to a PDF file. The URL is referenced on hundreds of websites. The URL doesn’t exist anymore. Way to go, Intel.
Everything we know about CRC but afraid to forget [(sic)]- https://crcutil.googlecode.com/files/crc-doc.1.0.pdf (Warning: idiotic google code URL auto-downloads the PDF instead of letting the browser display it. I’ve got about five copies of that PDF in my Downloads directory now.)
http://srecord.sourceforge.net/crc16-ccitt.html — more CRC-16-CCITT details.
CRC-16-CCITT — http://en.wikipedia.org/wiki/Computation_of_cyclic_redundancy_checks#Bit_ordering_.28Endianness.29 I translated this CRC-16-CCITT pseudocode from wikipedia into the self-contained CRC-16 implementation for crc16speed.
Fast with native CPU instructions (CRC-32 only) http://www.drdobbs.com/parallel/fast-parallelized-crc-computation-using/229401411
This is how you comment files: http://andrewl.dreamhosters.com/filedump/crc64.cpp — too bad the actual code formatting is beyond ugly.
http://users.ece.cmu.edu/~koopman/pubs/KoopmanCRCWebinar9May2012.pdf — CRCs in the air!
When I was down the rabbit hole of why hasn’t anything I’ve randomly changed resulted in success yet, I discovered the “Reflect” parameter of the CRC variant matters (CRCs deal with both inversion and reflection). Reflection matters a lot. It’s wild and crazy and it’s also what convinced me to find an existing implementation instead of trying to re-write it myself. CRC reflect insight: http://www.barrgroup.com/Embedded-Systems/How-To/CRC-Calculation-C-Code
Finally, crcspeed gained its final ability to self-host CRC-64-Jones thanks to pycrc: a python toolkit, CRC library, and code generation package. pycrc has internal models for many CRC variants and it has a simple way to generate clean C implementations of built in models. https://www.tty1.net/pycrc/ — https://github.com/tpircher/pycrc
fin.
BONUS ROUND
Mark’s slicing-by-8 implementation actually starts with:
while (len && ((uintptr_t)next & 7) != 0) {
crc = little_table[0][(crc ^ *next++) & 0xff] ^ (crc >> 8);
len--;
}What is that doing? If we’re processing 8 bytes at once, why do we need to process bytes before we start?
That initial while loop is actually completely optional. The only thing it does is process bytes individually (using the byte-by-byte lookup table) until we reach a pointer aligned to an 8-byte boundary.
That’s the magic of (uintptr_t)next & 7 — value & 7 is 0 only when value is a multiple of 8.
Why do we care about multiples of 8? Well, this is a process-8-bytes-per-loop method. For best performance, we want to process 8 bytes aligned to 8 byte boundaries. This is a pure performance optimization, not a correctness requirement. Removing the initial pre-alignment loop doesn’t change any results.
How does alignment change performance?
BONUS ROUND BONUS BENCHMARKS
For benchmarking the effect of data alignment on 8 byte processing, I removed the CRC-64 built-in alignment loop and fed the CRC-64 function unaligned data and perfectly aligned data.
Unaligned (One byte past 8 byte alignment)

See how noisy the graph looks? This is a graph of 1,000 CRC-64 calls with the input aligned one byte past an 8 byte alignment. The Y-Axis is the speed of the lookup in MB/s.
Aligned (exactly 8 byte alignment, (ptr & 7) == 0)

The second graph looks much better. All the results are high performing and there aren’t random spikes hanging too low.
But, what about the actual distribution of speeds in each case?
Unaligned vs. Aligned
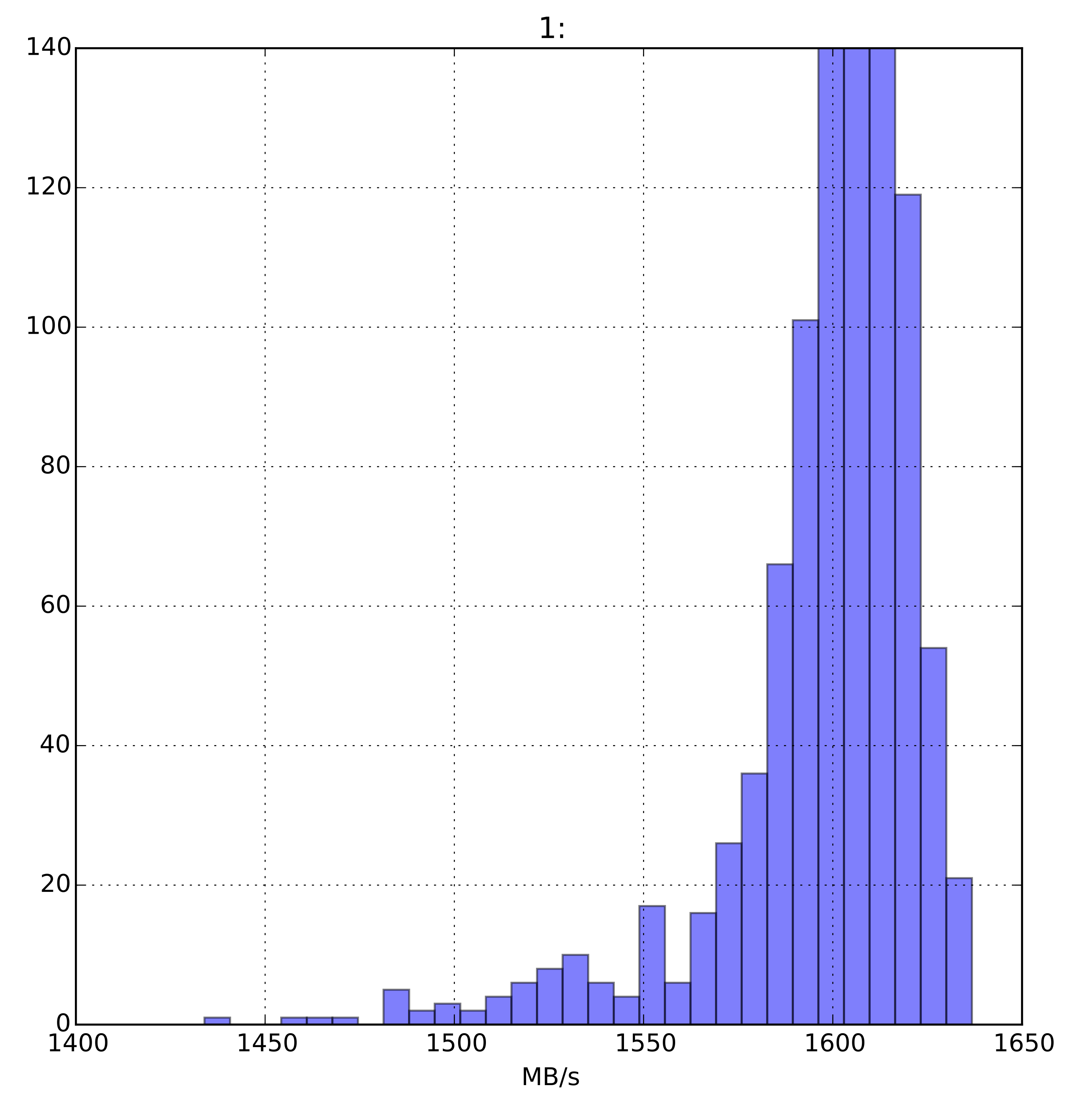

The first histogram is unaligned results. Notice it weights towards slower results. For unaligned access, the fast range isn’t guaranteed.
The second histogram is aligned results. Notice it looks almost like a perfect normal distribution.
Actually, if we look at the numbers, the kurtosis of the results are:
In [56]: df['1:'].kurtosis()
Out[56]: 6.9428038186302832
In [57]: df['7:'].kurtosis()
Out[57]: 1.1843067942858549Which is kinda amazing. All we did is run 1,000 results and, when perfectly aligned, we get an almost perfect Gaussian distribution of calculation speeds.
The aligned result also has the lowest variance of any byte alignment and the largest minimum as compared with the unaligned version.
Minimum throughput for off-by-one alignment: 1,433 MB/s
Minimum throughput for 8-byte alignment: 1,537 MB/s
Since we are processing our data in 8 byte steps, ensuring our data is aligned to an 8 byte boundary before looping 50 million times helps us guarantee better minimum performance with less variance as compared with just throwing randomly aligned data into the loop and hoping the system does the best all by itself.
Reminder for students: a byte is 8 bits. The maximum value for 8 bits is: 11111111 = 255 in base 10. So, to generate every possible 8 byte value, we only need 256 entries to represent 0-255. The initial CRC-64 lookup table is exactly 256 entries because it holds the CRC-64 result for each possible single byte value.↩
We should be careful calling the lookup table method “slow” because traditionally we use bit-by-bit computation running 400% slower than using a lookup table. But, compared to the new method running 400% faster than the lookup table, the lookup table is slow (and the bit-by-bit processing is super duper slow).↩