Accelerating Encodings

(Still have a short attention span? See graphs at the bottom.)

This describes an extension to Redis Quicklist: Optimal Quicklist Performance and Memory Reduction using Dynamic Adaptive Inverse Rectified Non-Linear Units Over Integrals of Ziplists.

Background

Quick recap:

• When Redis Lists are represented as linked lists, each list entry has ~40 bytes of overhead/metadata.
  • Storing lots of small elements in a linked list is inefficient since your overhead grows faster than your data size.
• So, we use Redis Ziplists to store many small elements
  • Ziplists exist to greatly reduce pointer and metadata overhead for list elements. (Regular list: 40 bytes per entry overhead; Ziplist: 1 to 10 bytes per entry overhead)
• Ziplist performance is great when ziplists are small, but quickly gets worse when ziplists get large. Redis only stores small numbers of elements of small sizes in ziplists, then, for performance reasons, converts to a larger, but faster for most operations, linked list representation.
• Quicklist is a linked list of ziplists allowing us to retain the excellent memory efficiency of ziplists along with the performance of small ziplists for lists of any length since we chain individual ziplists together for unlimited length list storage.

If you read the previous Redis Quicklist post, you’ll notice the lack of any performance comparisons—only memory comparisons were shown.

Now it’s time for the performance comparisons.

(tl;dr—using length-based cutoffs to figure out maximum ziplist size is dumb since performance is determined by the entire ziplist size; use entire ziplist size instead instead of number of entries.)

First, let’s define some terms

Ziplist Geometry

• length of ziplist: number of entries in the list
• width of ziplist entry: the size in bytes of one ziplist entry

So, a single ziplist entry uses 1 * width bytes and the total ziplist byte count is the integral from 1 to length of the ziplist over the width of each ziplist entry plus a small constant factor for the ziplist metadata.

Ziplist Neuron

• a rectified linear unit is defined as the maximum of either I or J: max(I, J)
• an inverse rectified linear unit is the minimum: min(I, J)

Dynamic Adaptive Inverse Rectified Non-Linear Units

Inputs

• integral of ziplist
• a default maximum ziplist size

Output

The output of a DAIRLU is either the current total ziplist size or the default maximum ziplist size. We run the output of the DAIRLU through a non-linear threshold neuron to generate a binary, non-stochastic, output determining whether or not we are allowed to populate this ziplist.

Previously

The old way: define a static ziplist length, with no regard for size of entries. A ziplist length of 10 could be storing 10 small integer entries of 1 byte each (total ziplist size: 10 * (1 byte data + 1 byte overhead) + 11 bytes ziplist metadata = 33 bytes) or 10 entries of 5 MB each (total ziplist size: 10 * (5 MB data + 10 bytes overhead) + 11 bytes ziplist metadata = 50,000,111 bytes).

The performance of a ziplist is directly related to the size of the entire ziplist; performance has nothing to do with the number of elements in the ziplist. A ziplist with 100 entries of 1 byte each performs better than a ziplist with 20 entries of 5 MB each¹.

How we Can Improve Upon Previously

What we need is two parameters:

• maximum ziplist length
• maximum ziplist size

If you define a maximum ziplist size instead of a static ziplist length, the length of every ziplist becomes dynamic. The size of a ziplist is allowed to grow until it reaches your size limit, which adapts the ziplist to the most efficient use of your specified memory limit. If a ziplist tries to grow beyond your size limit, a new ziplist gets created to keep all ziplists at a fast size.

If you define a maximum ziplist length and we allow ziplists to be capped to a maximum size, entries are added to the ziplist unless they would grow the ziplist over a safe default maximum size. Using an explicit length with an implicit size cap allows you to tune ziplist performance faster (maybe; depends on your use case), at the expense of a little memory usage, while still having a safety limit to automatically stop any individual ziplist growing too big.

Now

Previously the only quicklist ziplist user-specified parameter was ziplist length, but now the length has two options and one safeguard:

• If requested length is 1 or larger, use that ziplist length, but also apply a safety ziplist maximum size of 8k for the entire ziplist.
• If requested length is negative, use only ziplist size-based allocation for one of five different size classes:
  • Length -1: 4k
  • Length -2: 8k
  • Length -3: 16k
  • Length -4: 32k
  • Length -5: 64k

So, when using a positive ziplist length and inserting an element into a ziplist: we apply the inverse rectified linear unit to the integral of the ziplist along with 8192, run that result through our non-linear threshold unit, then we know if we should create a new ziplist for this element or add it to an existing ziplist.

For requesting an exact maximum ziplist size, we dynamically adapt the number of entries per ziplist so every ziplist makes the most efficient use of memory as possible without requiring any user parameter adjustments based on the shape of user data. Any elements larger than the maximum ziplist size will be created in their own ziplist node so they don’t cause a performance impact on any other ziplist.

Usage Guidelines

You should always benchmark your individual use cases with elements the sizes of your production data distribution, but a good starting point is:

• Just use a value of -2 which allows each ziplist to grow to a maximum of 8k.
• If you have more demanding use cases, you can use explicit list lengths to store fewer than 8k of data per ziplist, but if your data misbehaves, you will still be protected from poor performance by the implicit 8k total ziplist size safety limit.
  • Setting an explicit length allows you to get faster list operations (maybe; test it yourself for your use cases) because your ziplists will remain smaller for memory allocations.

Those are the standard use cases, but what about lists of big elements?

What if we are storing a list of 10,000 entries and each entry is 10 MB? Or, what if we are storing wildly varying data with the size of list entries being rougly Gaussian with mostly small elements, but also with a few outlier elements of hundreds of MB each?

The dynamic adaptive quicklist ziplist interface will notice that adding a 10 MB entry can’t possibly fit into anything you requested since it’s above all explicit size limits (4k to 64k) and it’s above the default safe growth limit of (8k), so each large element gets placed in its own individual ziplist—and that’s exactly what we would want to happen, it gives the best performance in a dynamically adaptive way.

Results

Y-Axis: requests-per-second

X-Axis: ziplist length parameter given to quicklist. “ORIGINAL” is the Redis Linked List implementation with no quicklist or ziplist involvement.

“ORIGINAL” is usually faster (but not always!), but not by much, plus the quicklist can give you 25% to 12x memory reduction at the cost of just a little throughput in some cases (and not in others).

[single] RPOP and LPOP of 40 byte elements

Before (length-only)

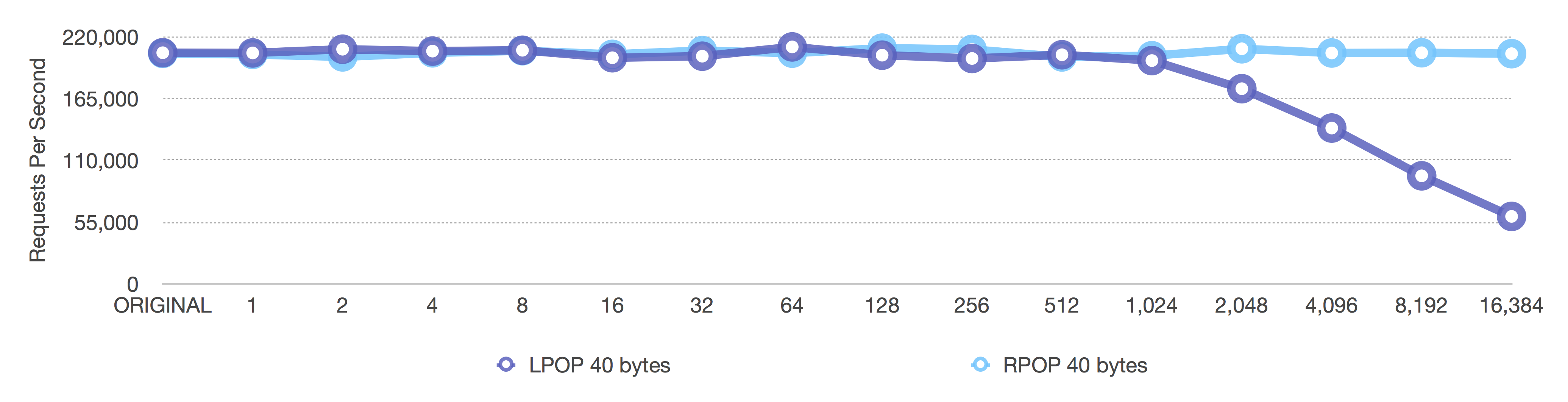
After (adaptive, negative = fixed sizes, positive = length OR 8k max size)

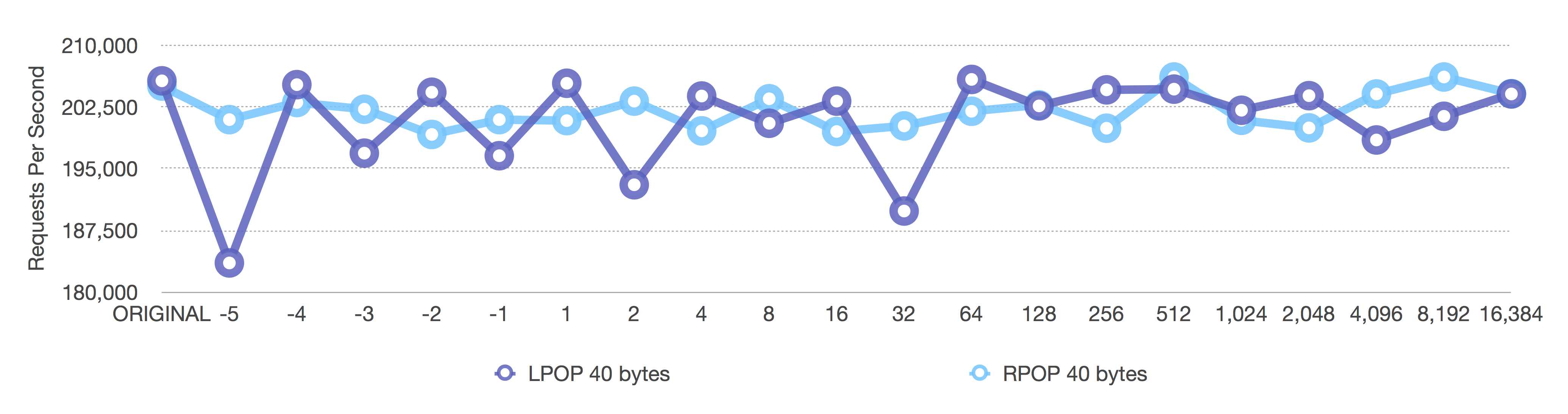
The second graph looks more noisy, but that’s because the Y-axis on the second graph is much tighter than on the first graph.

Notice how on the first graph the LPOP decreases when the ziplist size gets too big— that’s because removing the head (left, LPOP) of a ziplist requires moving the entire ziplist up just one element after we remove the head. We want to reduce the impact of that copying as much as possible, as we do in the second graph.

[single] RPOP and LPOP of 1k byte elements

Before (length-only)

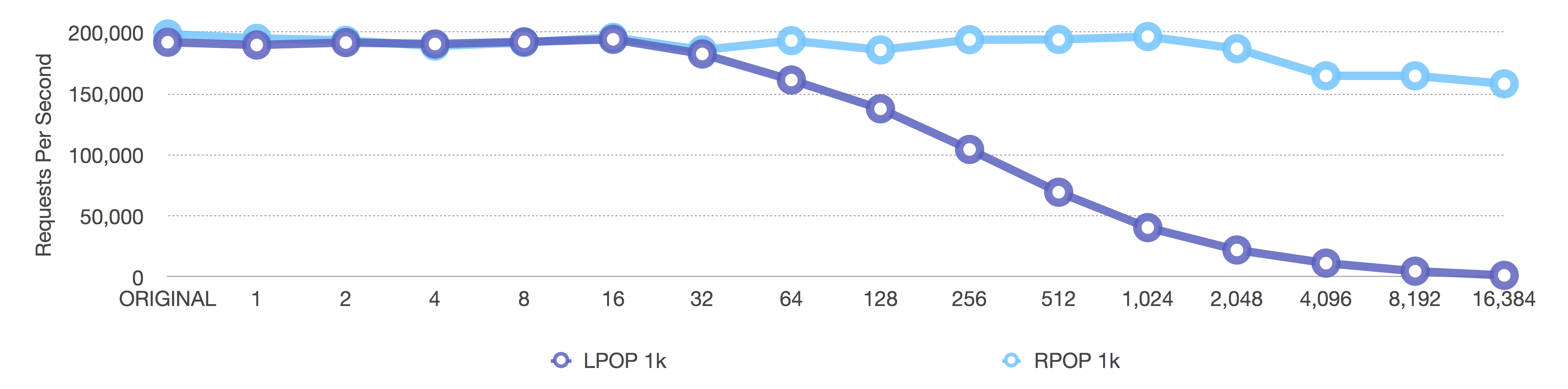
After (adaptive, negative = fixed sizes, positive = length OR 8k max size)

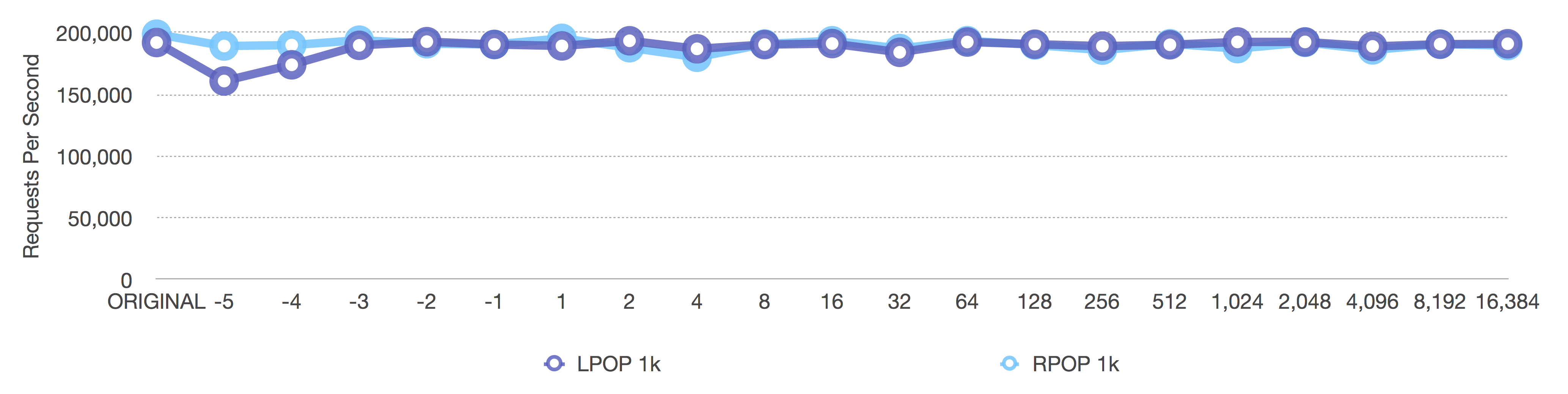
We see the same effects here, except, with 1k elements, the original dropoff happens much sooner. This comparison also has equal axes across both graphs, so the results are easier to compare.

In a way, the dynamic adaptive ziplist is both lying and protecting the user at the same time. If you specify a ziplist length of 1024 and you insert 1k elements, you’ll never achieve a ziplist length of 1024 elements since that would be 1024*1k = 1MB. It ends up being exactly the same as specifying a ziplist length of -2 (which defaults to a maximum 8k size for the entire ziplist)—we just protected the user from itself.

Now let’s look at the same operations, but in a longer pipeline instead of a single request/response per run.

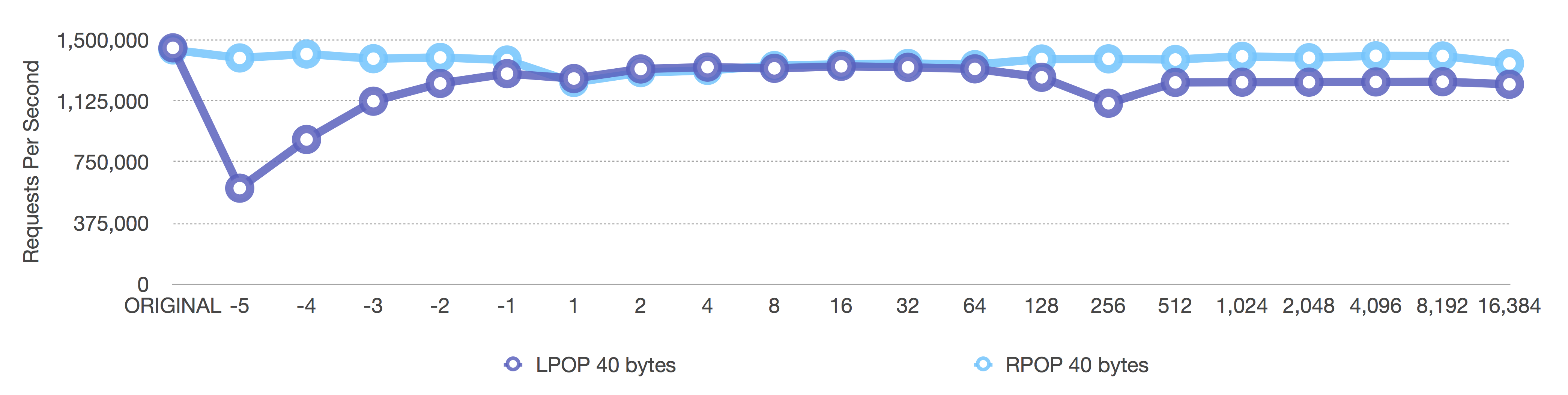
[pipeline of 1,000 requests] RPOP and LPOP of 40 byte elements

Before (length-only)

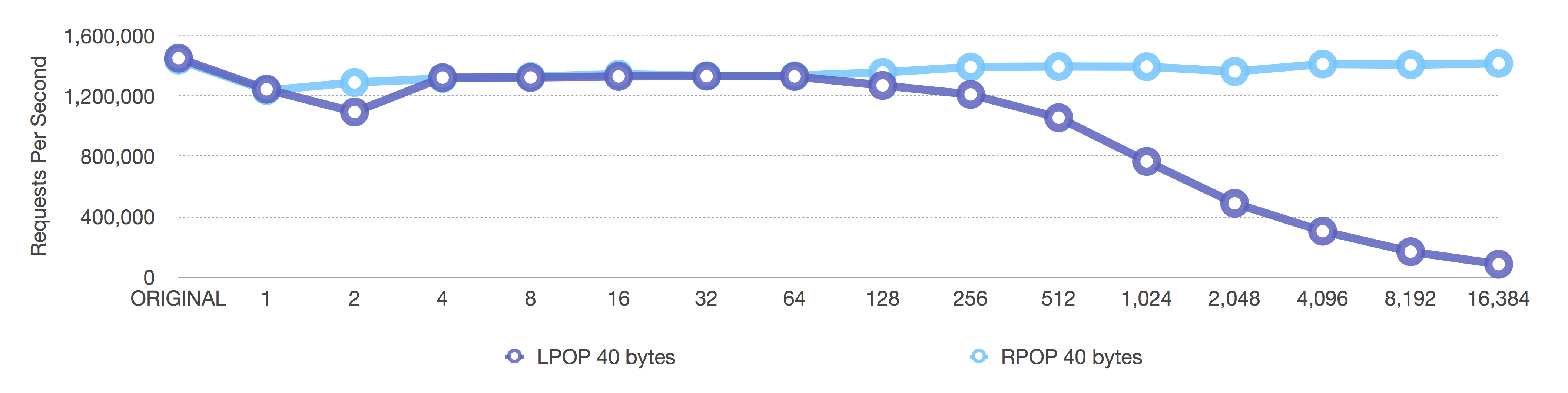
After (adaptive, negative = fixed sizes, positive = length OR 8k max size)

Notice the Y-axis here as well. Because we are running a pipeline of 1,000 requests, we get Redis to do close to 1.5 million removals per second for small 40 byte values.

The Before graph shows the dropoff we expect, but it happens a little earlier than the [single] graph above because in the [single] graph, a lot of noise is created by the individual network processing for each request. When we run a pipeline of 1,000 requests, we get a better picture of how Redis is performing versus how the networking stack is performing.

[pipeline of 1,000 requests] RPOP and LPOP of 1k byte elements

Before (length-only)

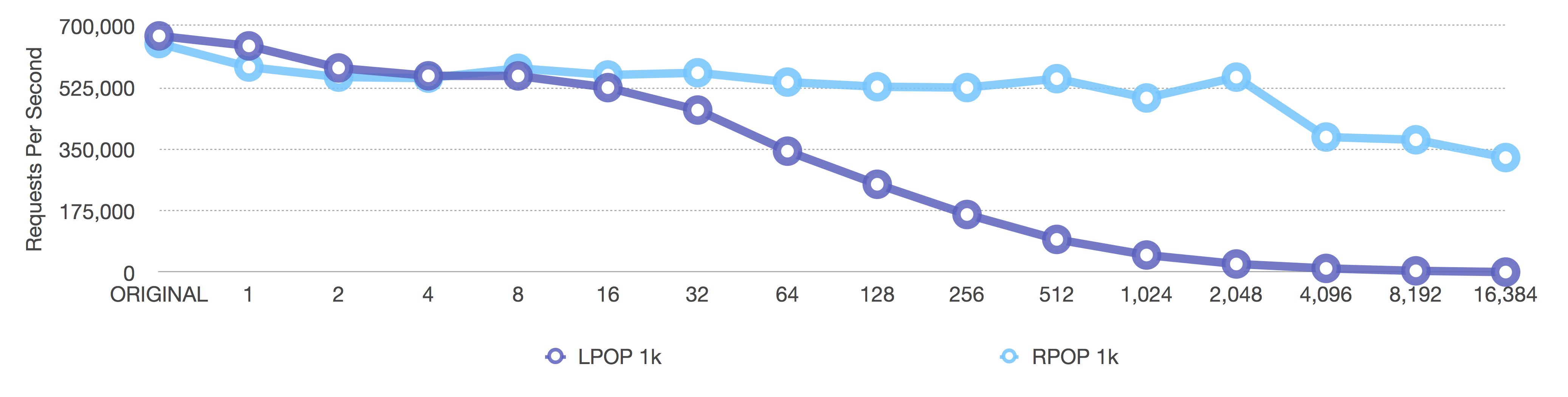
After (adaptive, negative = fixed sizes, positive = length OR 8k max size)

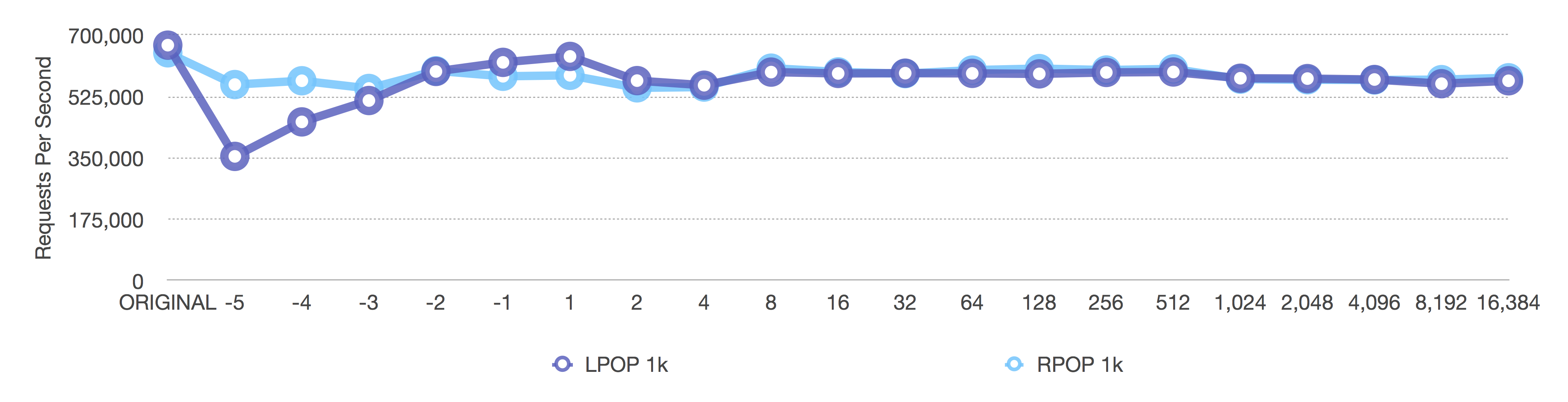
The same happens here as in all the previous graphs, but note how the operations per second are around 600,000 instead of 1.5 million for larger values. Larger values require more processing time than smaller values.

Memory Usage

Finally, a quick review of memory usage.

LPUSH/RPUSH of 40 bytes

Before (length-only)

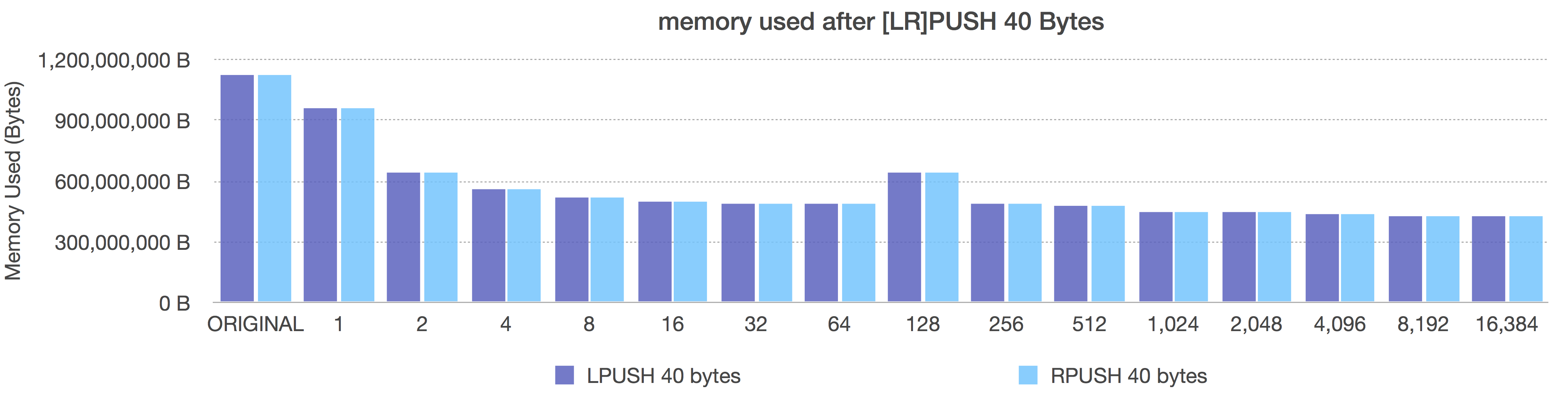
After (adaptive, negative = fixed sizes, positive = length OR 8k max size)

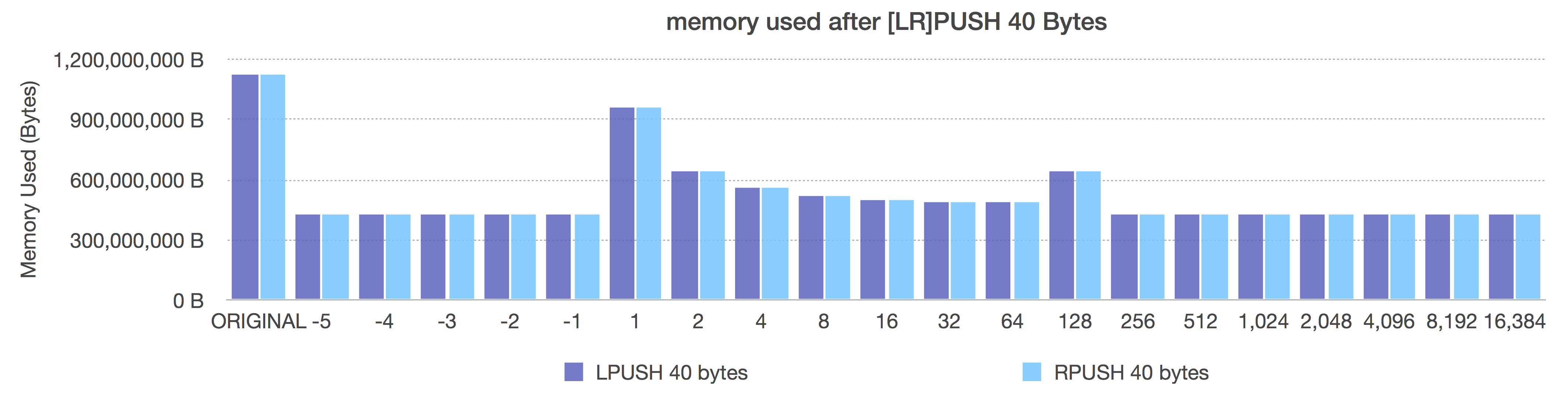
In the Before graph, we see the expected pattern of memory decreasing with ziplist length (because more elements per ziplist means less pointer overhead).

In the After graph, we see the size-based ziplist representations each immediately give us the best memory utilization. They all use the same memory because using size classes instead of length lets dynamically pack each ziplist with the most entries for that size class giving us (provably) the most adaptive memory savings due to pointer removals.

LPUSH/RPUSH of 1k

Before (length-only)

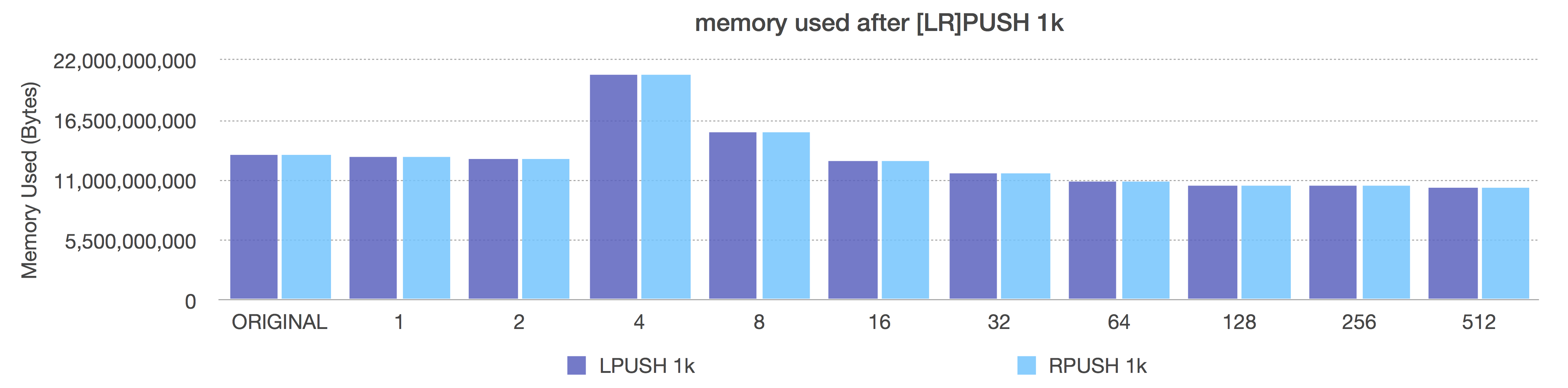
After (adaptive, negative = fixed sizes, positive = length OR 8k max size)

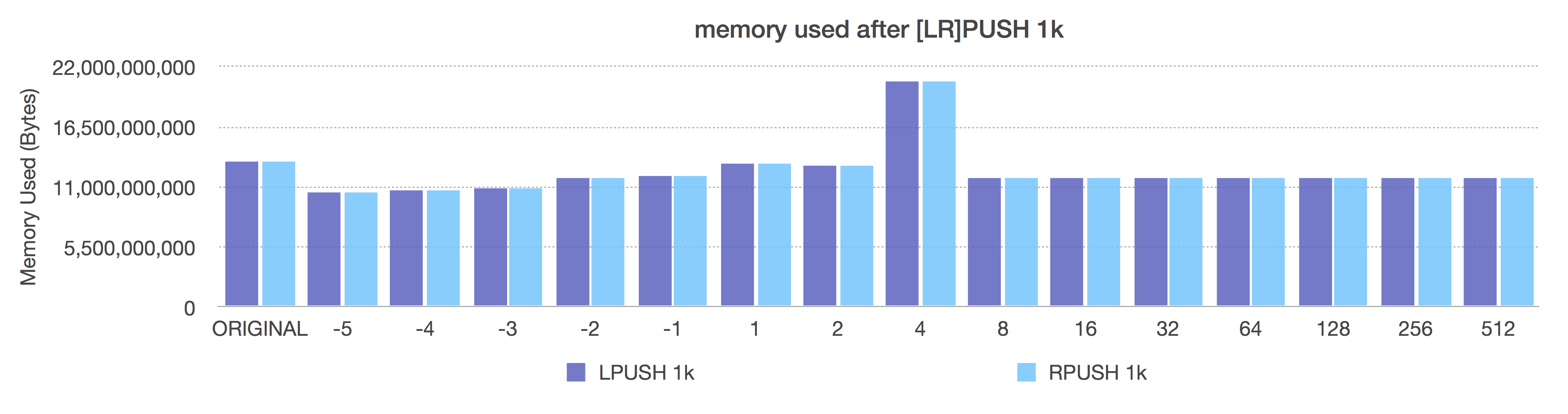
Look carefully at the After graph here. Notice here that size class -5 (64k ziplists) gives us the best overall space savings (reminder: these are 1k inserts). That looks great, right? But go up to the previous request-per-second graphs and compare the speed for a 64k ziplist too. It’s pretty awful. So, here, even when using large elements, you do not probably want to not go all the way down to -5.

Also notice how, when using 1k elements here, the ziplist length of 8 is exactly equal to the performance of size class -2. That’s because if you add 8 entries each of 1024 bytes to a ziplist, you spill over 8k (due to small ziplist overhead), so your ziplists all get limited to the implicit safety limit of 8k, even at size 8, which makes your size class equal to a fixed ziplist size of -2 (8k).

You can also easily pick the correct quicklist size class for your own use cases. If your use case is always appending to lists using RPUSH along with a heavy read workload, you can use size classes that use the best storage + the best appending performance. If your use case is appending and removing from both sides of the list all the time, you can pick a size category or a list length to optimize performance vs. memory utilization.

Got it?

But WHY?

Why those size classes? Why does any of this work at all? Why prefer 8k implicit ziplist sizes instead of 4k or 16k or 32k? Why is the sky bleeding purple ooze?

I’ll just leave you with one more graph. Draw your own conclusions.

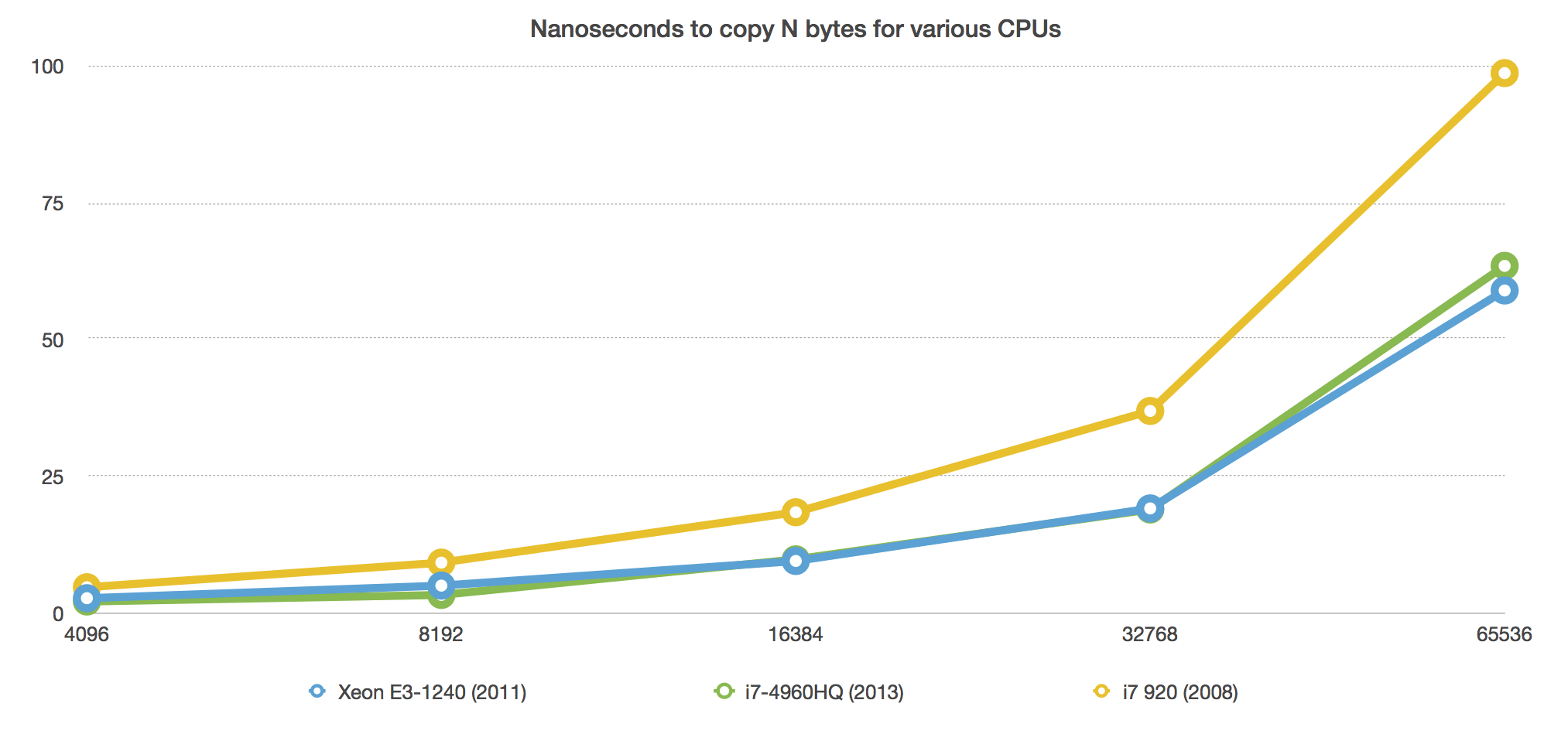
Packaged Results

You can find the full results for each test run at:

• Numbers sheets (1 MB) with result tables and graphs
• PDF export of numbers sheet (11 MB)

All tests were run by starting a redis-server, running redis-benchmark in pipeline (or not) with 10M (pipeline) or 1M (single) requests. After each test, the server is killed and we start over. Every test case is run with an empty, fresh, clean server.

Next?

There are two or three additional micro-optimizations we can make to get a few more percentage points of improvement for quicklist request-per-second operations, but those will wait for another day.

---

1. Small ziplists perform better because any insert or removal to the head of the ziplist requires moving all subsequent memory down. Remember, ziplists are solid blocks of memory, so inserting into the head of a ziplist means everything else has to be moved down to make room for your new entry. The most efficient ziplist operation is appending and removing the tail of the ziplist, while the worst operation is inserting or removing the head of the ziplist.↩